Niveau mit Graphpak

Einfache Liniendiagramme, die Erstellung von Graphen für Funktionen in einer reellen Variablen, sind mit Graphpak mehr als trivial. Ein oder zwei Zeilen, und schon sehe ich den Funktionsverlauf, so kompliziert die Funktion auch sein mag.

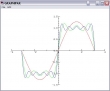
Die Darstellung von Funktionsfolgen ist kaum schwieriger:

x←¯10 to 10,0.1

PLOT x,⊃[1](⍳n)s¨⊂x

Das ist alles.

Bis hier braucht man kein Handbuch, für das Folgende ist die Konsultation des Graphpak Users's zu empfehlen: Der Visualisierung von reellen Funktionen in zwei Veränderlichen auf dem ebenen Bildschirm.

Da wäre als erste Darstellungsform das Höhenlinien- oder Niveaudiagramm, in Software gegossen als Graphpak-Funktion CONTOUR. Um die Konturen auf den Höhen -2,-1,0,1,2 für die Funktion f(x,y) zu zeichnen, gehe man wie folgt vor:

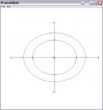
x←y←¯5 to 5,0.1

m←(x BY y) OF x∘.f y

m[1;1]←1

¯2 ¯1 0 1 2 CONTOUR m

AXES

LABEL

Zwei Nieveaulinien "fehlen". Warum wohl?

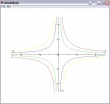
Mit einer anderen (mathematischen) Funktion kommen auch diese zum Zuge. Mit ein wenig mehr Arbeit lassen sich die Höhenlinien unterschiedlich einfärben: Variable pa setzen und CONTOUR mit jeweils einem Niveau im linken Argument aufrufen. Keine Sorge, dass passt solange svp unverändert bleibt.

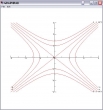
Für welches f(x,y) sind das wohl die Niveaulinien?